2-site DMRGを試してみて基底状態のエネルギーが算出できましたよと言いたかった記事です。（実装でどこか間違っていて参考にしたやつの結果とは一致しませんでした。）

概要

計算科学などの領域で使用できる高水準言語で最近注目されている Juliaを用いて２サイトDMRG法の実装を試した。Juliaが注目される理由と、DMRGの概要、その実装について大まかな流れを記載していきます。

Juliaが注目されている理由

Juliaはここ最近、数値計算界隈で注目を集めています。
注目を集めている一番大きな理由としては、インタプリタであるにも関わらず、C言語に迫る計算スピードがあることではないでしょうか。とにかく早いです。

また、pythonで記述されている関数をインポートできたり、数値計算用のライブラリも増えてきているようなので、ユーザーが増えているみたいです。
あまり日本で使っている人は少ないので、今のうちに習得しちゃってつよつよの人材になっちゃいましょう。

DMRGの概要

密度行列繰り込み郡法

イジングモデルやハイゼンベルグモデルの基底状態を近似的に求める際にしようされてきたアルゴリズムです。
こういった数値計算では、対象の系が大きくなると、状態数が指数関数的に大きくなり、厳密解を求めるにはメモリが足りなかったり計算時間が膨大になるなどの問題が発生します。

DMRGでは密度行列を計算し、その固有値が高い順に一定数の状態のみを保存することで状態数を制限し、厳密解に非常に近い近似解を少ない計算で求めることができます。

また、DMRGはテンソルネットワークや行列積状態の最適化に応用できることがわかっています。今回は2-site DMRGを実装してみました。

DMRGのステップ

①　量子状態を行列積状態に変換
②　ハミルトニアンを行列積演算子に変換
③　左端のサイトから右端のサイトへ局所的に最適化
④　右端のサイトから左端のサイトへ局所的に最適化
⑤　③④を繰り返す

量子状態を行列式状態(MPS)に変換

サイト数Lの量子状態を行列積状態に変換します。
最終的に以下のような形に変換していきます。

\ket{\psi} \ = \sum_{\sigma_1 ...,\sigma_L} c_{\sigma_1...,\sigma_L} \ket{c_{\sigma_1...,\sigma_L}} 

　　　　　　　　　　↓

\ket{\psi} \ = \sum_{\sigma_1 ...,\sigma_L} A^{\sigma_1}A^{\sigma_2}...A^{\sigma_L} \ket{c_{\sigma_1...,\sigma_L}} 

ステップ１　状態ベクトルを(d × d^L−1)の行列に変形

\psi_{\sigma_1(\sigma_2 ...,\sigma_L)} \ = c_{\sigma_1...,\sigma_L}

ステップ2　SVDで分解、真ん中の対角行列とVをかける

c_{\sigma_1...,\sigma_L} = \psi_{\sigma_1(\sigma_2 ...,\sigma_L)} = \sum_{a_1}^{r_1}U_{\sigma_1,a_1}S_{a_1,a_1}(V^{\dagger })_{a_1,(\sigma_2...,\sigma_L)} \equiv  \sum_{a_1}^{r_1}U_{\sigma_1,a_1}c_{a_1,(\sigma_2...,\sigma_L)}

ステップ3　ステップ2を右端まで繰り返す。

ハミルトニアンを行列積演算子(MPO)に変換

計算結果がすぐ判断できるように、今回使用するハミルトニアンはシンプルに隣り合うz軸方向のスピンを掛け合わせたものにします。

\hat{H} = \sum_{i=1}^{L-1} \hat{S}_i^z\hat{S}_{i+1}^z

まずL=9サイトの時を試してみます。
行列は以下のように書き換えられます。

\begin{bmatrix}
0 & S_1^z & I_1 \\
\end{bmatrix}
\begin{bmatrix}
I_2 & 0 & 0 \\
S_2^z & 0 & 0 \\
0 & S_2^z & I_2 \\
\end{bmatrix}
・・・
\begin{bmatrix}
I_8 & 0 & 0 \\
S_8^z & 0 & 0 \\
0 & S_8^z & I_8 \\
\end{bmatrix}
\begin{bmatrix}
I_9 \\
S_9^z \\
0
\end{bmatrix}

左端のサイトから右端のサイトへ局所的に最適化

MPOとMPSに変換したハミルトニアンと量子状態に対して縮約をとっていき左側2サイトを残した状態の局所的なハミルトニアンを作成します。

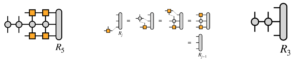
作成したハミルトニアンに対して、最適化を行い、状態ベクトルをMPS状態に変換します。

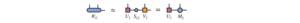
最適化した左端のサイトに対して縮約をとり、次の局所的なハミルトニアンを作成します。

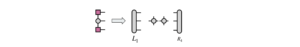
先ほどと同様に最適化された状態ベクトルをMPS状態に変換します。

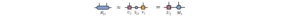
この作業を右端のサイトまで実行します。

右端のサイトから左端のサイトへ局所的に最適化

上で行った作業を今度は右端のサイトから左端のサイトまで順番に実行します。

上記の作業を繰り返す

局所最適化をエネルギーが収束するまで実行することで、基底状態を探すことができます。しかも少ない状態数しか扱わずに！

結果

初期状態は全て上向スピンでそろっているものとしました。
少しずつエネルギーが下がっていっていますが、途中上がることもあります。。。どこか実装を間違っているようですね、、、引き続き調査していきます。

E0=6.0 + 0.0im
E0=6.0 + 0.0im
E0=6.0 + 0.0im
E0=6.0 + 0.0im
E0=6.0 + 0.0im
E0=6.0 + 0.0im
E0=6.0 + 0.0im
E0=6.0 + 0.0im
E0=4.0 + 0.0im
E0=4.0 + 0.0im
E0=0.0 + 0.0im
E0=0.0 + 0.0im
E0=-4.0 + 0.0im
E0=-4.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-6.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im
E0=-8.0 + 0.0im